Cusp Catastrophe How-to

by W. Garrett Mitchener

In this worksheet, I illustrate how to generate a bifurcation diagram for a two-parameter dynamical system in one dependent variable.  The particular types of bifurcations that can happen form what's called a cusp catastrophe.  This worksheet shows several ways to generate the cusp picture that illustrates what happens.

Setup

Let's work with the dynamical system given by:

First, here's how to define a function for the right hand side:

In[1]:=

Out[1]=

First method: Solve for fixed point collision directly

Fixed points happen when , and bifurcations happen when fixed points collide (and in other situations).  But look what happens when we try to solve for the fixed points:

In[2]:=

Out[2]=

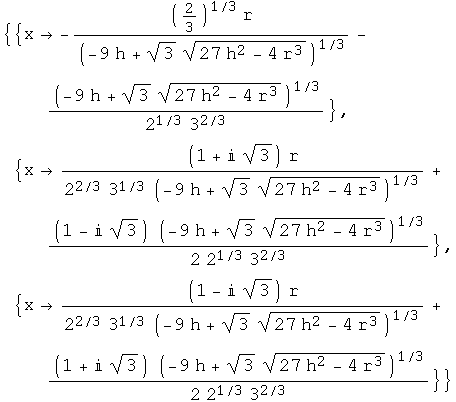
Those expressions are pretty nasty, and you can't tell which roots are real or complex.  Don't let the i's in those two lower expresssions fool you.  The square roots may generate complex numbers depending on and that cancel out with the i's on top.  For the moment, suppose that's not a problem.  Now imagine trying to set two of these equal and solve for and :

In[3]:=

Out[3]=

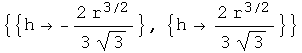
We got lucky: That's the right answer, and the computer didn't crash. I don't recommend this method because if your dynamical system is more complicated than this example, the expressions for the roots will probably be so big and complicated that Mathematica can't deal so easily with them.  It's worth a try in that case, but there are alternatives.  I'll plot the solution below, after showing an alternative method of deriving it.

Second method: Combine fixed point solve with linear stability analysis failure

An alternative is to use the fact that Mathematica can handle systems of polynomial equations very easily.  Here, we Solve for the parameter values such that there is a fixed point at , and such that linear stability analysis fails there.

In[4]:=

Out[4]=

We want to plot horizontally and vertically to reproduce the figure on p. 71 of Strogatz.  The nice thing about this result is that it gives and very simply in terms of the fixed point , so we can vary , and generate a plot of vs. parametrically.  Here's how to set that up.

Just so you'll know, the solution comes as a list of rule tables, because some systems of equations may have many solutions.  So we use to fish out the single rule table we want:

In[5]:=

Out[5]=

Then we have to make an expression for ParametricPlot.  

In[6]:=

Out[6]=

Finally, here's the plot command:

In[7]:=

Out[7]=

Just so we can see the cusp more clearly, here's a set of plotting options (see 1.9.2) that moves the axes, and sets the aspect ratio so the vertical axis isn't squished:

In[8]:=

Out[8]=

By the way, I just guessed that should go from -5 to 5.  Alternatively, you could solve for the fixed points explicitly for (the right-hand edge) and get an idea for the range that way.

Third method: Discriminants

Every polynomial has a discriminant.  (See http://mathworld.wolfram.com/PolynomialDiscriminant.html.)  The definition is kind of complicated:  You start by numbering all the roots of a polynomial .  Remember, every complex polynomial of degree has complex roots.  Then the discriminant is defined to be the product of the squares of the differences between every possible pair of roots:

So the discriminant is zero if two of the roots coincide.  Luckily, there's a way to compute the discriminant just from the coefficients of the polynomial.  The following incantation defines such a calculation.  (Don't worry about how this works for now.)

In[9]:=

Here's the familiar discriminant for a quadratic polynomial, up to a factor of :

In[10]:=

Out[10]=

So if our function undergoes a bifurcation at parameter values and , two fixed points collide, which means the discriminant must be zero:

In[11]:=

Out[11]=

The equation defines a curve in the implicitly, and we want to get a picture of it.  There are different ways to do this.  One is to use ImplicitPlot.  We have to first load a package to make that command available.

In[12]:=

In[13]:=

Out[13]=

An alternative is to solve for one variable in terms of the other.  This can get a little tricky:

In[14]:=

Out[14]=

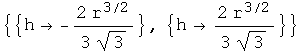
Now we need both solutions.  This expression gives us a list of solutions for :

In[15]:=

Out[15]=

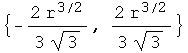
The /. command can work with a list of rule tables, and produces a list of what happens when you apply the different rule tables to the expression on the left.  Just so you see what it's doing:

In[16]:=

Out[16]=

Now for our plot.  Since we have as a function of , we can use the regular Plot command, but we need to plot both solutions.

In[17]:=

Out[17]=

That isn't good.  What sometimes happens is that Mathematica evaluates the expression you're plotting in a funny order, so for example, it sets , and looks at but doesn't evaluate the /. substitution, so there's nowhere to plug in , and it gets confused.  What usually works in this case is to tell Mathematica not to delay evaluating the expression to be plotted.  You do that by wrapping it in Evaluate.  This is a good trick to know.  Solve, Plot, and other functions are documented as having this odd behavior: They "evaluate their arguments in a non-standard way" which is a clue that you might need to use Evaluate.  Anyway, here's the repaired Plot command:

In[18]:=

Out[18]=

By the way, you can ignore the complaints about not getting a real number.  The plotting process complains because the expression generates complex numbers for and nothing bad happens; they just don't show up in the plot.

We can also solve for as a function of , which happens to be easier in this case.

In[19]:=

Out[19]=

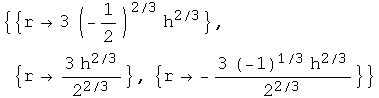
Two of the solutions are complex for every , so the only one we need to worry about is:

In[20]:=

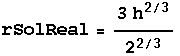
Out[20]=

And here I've just used the mouse to select the one I want from the output, and copied it to an input cell.  Now it should be clear why we get a cusp: Functions of the form for have cusp-shaped graphs.  The plot is a little weird:

In[21]:=

Out[21]=

The left hand side is missing and we get complaints about not getting real numbers for negative values of .  That's because Mathematica is extremely careful with complex numbers, and knows that is generally not well defined for negative .  The case of is an obvious example.  So we end up getting only half the plot we wanted.  The parametric form is better because it doesn't have this problem.

Fourth method: Template polynomials

Just so you'll know, "template polynomial" is a term I made up.  As far as I know, there's no standard name for this technique.

We suppose that a bifurcation occurs at such that two fixed points coincide.  That means there's a double root.  So, to trace out such values of and , we set our equal to a polynomial with the same degree, and same highest-power coefficient, but with overlapping roots.  That's what I call the template:

In[22]:=

Out[22]=

Here, and are the two roots, and by putting in , I've specified that is a double root.  I put in the sign because the highest-order term of is and the template has to match that.  To make use of this template, what we need to do is equate the coefficients of our template to the coefficients of .  That gives a bunch of equations for and .  We can get the coefficients by using the CoefficientList function:

In[23]:=

Out[23]=

In[24]:=

Out[24]=

In[25]:=

Out[25]=

We now need to turn these into a list of equations.  The Thread function is used to turn a function of two lists into a list of functions of pairs:

In[26]:=

Out[26]=

And it works with equations, too:

In[27]:=

Out[27]=

So we can equate our coefficients with the incantation:

In[28]:=

Out[28]=

Notice that we get a couple of easy equations.  First, the highest order coefficients are both because I defined them that way, so the last entry is which simplifies to True.  Second, we get out of the next highest, which is very nice.  That let's us get rid of p2 entirely.  This is easy enough to do by hand in this case, but Mathematica can also do it automatically.  We use the Eliminate function to get rid of .

In[29]:=

Out[29]=

I'd really rather have a list:

In[30]:=

Out[30]=

This is the same set of parametric equations we got before, so I won't plot them again.

Incidentally, suppose we wanted to find the parameter values where all three fixed points collide.  That's the pitchfork bifurcation.  Then we simply use a different template:

In[31]:=

Out[31]=

Now is a triple root.  We proceed as before, equating coefficients:

In[32]:=

Out[32]=

Now things are much more restricted:

In[33]:=

Out[33]=

By the way, I hope this last solution is obvious from the system of equations.

Created by Mathematica  (February 3, 2005)