CurveFittingHowTo.nb

Curve fitting How-to

by W. Garrett Mitchener

This worksheet goes over traditional linear and non-linear least squares curve fitting and different ways to do it in Mathematica. It also goes over maximum likelihood curve fitting. Along the way, it shows different functions for finding maxima and minima of expressions.

Least squares and linear regression

Let's say you have some data ${(x_1, y_1), (x_2, y_2) ...}$ and you want to fit a curve to it so that you can say .

To illustrate, let's create some noisy data:

In[1]:=

Out[1]=

RowBox[{{, RowBox[{RowBox[{{, RowBox[{-5, ,, RowBox[{-, 6.04965}]}], }}], ,, RowBox[{{, RowBox ... , ,, RowBox[{{, RowBox[{4.75, ,, 12.365}], }}], ,, RowBox[{{, RowBox[{5., ,, 13.7237}], }}]}], }}]

In[2]:=

[Graphics:HTMLFiles/CurveFittingHowTo_6.gif]

Out[2]=

In Mathematica, the Fit function takes a list of points, a list of expressions, and a list of independent variables, and determines which linear combination of the given expressions produces the best fit to the data. If you want to fit a line to the data, your list of expressions should consist of 1 and x, since a line is a linear combination of a constant and a multiple of x:

In[3]:=

Out[3]=

In[4]:=

[Graphics:HTMLFiles/CurveFittingHowTo_11.gif]

Out[4]=

In[5]:=

[Graphics:HTMLFiles/CurveFittingHowTo_14.gif]

Out[5]=

And you can see that we've more or less recovered the that we used to create the data in the first place.

You can also do more interesting things:

In[6]:=

Out[6]=

RowBox[{{, RowBox[{RowBox[{{, RowBox[{-5, ,, 1.03237}], }}], ,, RowBox[{{, RowBox[{RowBox[{-, ... 5, ,, RowBox[{-, 1.24612}]}], }}], ,, RowBox[{{, RowBox[{5., ,, RowBox[{-, 1.16977}]}], }}]}], }}]

In[7]:=

[Graphics:HTMLFiles/CurveFittingHowTo_20.gif]

Out[7]=

For instance, this fits a second degree polynomial to the data:

In[8]:=

$poly2fit = Fit[data2, {1, x, x^2}, x]$

Out[8]=

$RowBox[{RowBox[{0.0168822, }], -, RowBox[{0.0792803, , x}], -, RowBox[{0.000863356, , x^2}]}]$

In[9]:=

[Graphics:HTMLFiles/CurveFittingHowTo_25.gif]

Out[9]=

Not a very good fit, is it? It doesn't have nearly enough bumps. Let's try something higher degree.

In[10]:=

$poly5fit = Fit[data2, {1, x, x^2, x^3, x^4, x^5}, x]$

Out[10]=

$RowBox[{RowBox[{-, 0.00380876}], +, RowBox[{0.870284, , x}], +, RowBox[{0.00704091, , x^2}], -, RowBox[{0.11371, , x^3}], -, RowBox[{0.000351999, , x^4}], +, RowBox[{0.00285105, , x^5}]}]$

In[11]:=

[Graphics:HTMLFiles/CurveFittingHowTo_30.gif]

Out[11]=

That looks a lot better. I knew to guess 5 for the degree because the data goes through four extrema.

In[12]:=

[Graphics:HTMLFiles/CurveFittingHowTo_33.gif]

Out[12]=

But don't get carried away. If you give it too many degrees of freedom, it will start to fit the noise, as in this example:

In[13]:=

$powerTable = Table[x^n, {n, 0, 25}]$

Out[13]=

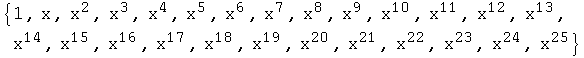
${1, x, x^2, x^3, x^4, x^5, x^6, x^7, x^8, x^9, x^10, x^11, x^12, x^13, x^14, x^15, x^16, x^17, x^18, x^19, x^20, x^21, x^22, x^23, x^24, x^25}$

In[14]:=

$General :: spell : Possible spelling error: new symbol name \"poly25fit\" is similar to existing symbols {poly2fit, poly5fit} . More…$

Out[14]=

$RowBox[{RowBox[{-, 0.0240747}], +, RowBox[{0.736313, , x}], +, RowBox[{0.059761, , x^2}], +, ... 384*10^-10, , x^23}], +, RowBox[{1.1405*10^-11, , x^24}], -, RowBox[{1.73697*10^-12, , x^25}]}]$

In[15]:=

[Graphics:HTMLFiles/CurveFittingHowTo_41.gif]

Out[15]=

You can also do more exotic things:

In[16]:=

Out[16]=

In[17]:=

[Graphics:HTMLFiles/CurveFittingHowTo_46.gif]

Out[17]=

but that doesn't look right somehow. In fact, I get vastly different plots every time I run this worksheet, which indicates that the random noise added to the data is having a huge impact on the cosine fit, which isn't the case for the fifth degree polynomial. That indicates that these cosines are not a good way to fit this data. (Think about it: Why?) The first step to getting a good fit is to know what functions to include.

Details on how Fit works.

The way Fit works is called least squares, because it minimizes this:

Underoverscript[∑, j = 1, arg3] (f[x_j] - y_j)^2

In Mathematica notation

In[18]:=

$LeastSquaresError[data_, f_] := Sum[(f[data[[j, 1]]] - data[[j, 2]])^2, {j, 1, Length[data]}]$

Let's return to our linear data.

In[19]:=

Out[19]=

RowBox[{{, RowBox[{RowBox[{{, RowBox[{-5, ,, RowBox[{-, 6.04965}]}], }}], ,, RowBox[{{, RowBox ... , ,, RowBox[{{, RowBox[{4.75, ,, 12.365}], }}], ,, RowBox[{{, RowBox[{5., ,, 13.7237}], }}]}], }}]

Here's how to define a general line function:

In[20]:=

Out[20]=

To fit this line to the data, we need to determine and such that the error is minimized.

Mathematica has several functions for finding the minimum of an expression. They all work a little differently. The Minimize function works algebraically:

In[21]:=

Out[21]=

The result is a list where min is the minimum value it found, and args is a rule table. Here's how to use a rule table. First, just so we're clear on what's going on, we'll unpack the list returned by Minimize.

In[22]:=

$General :: spell1 : Possible spelling error: new symbol name \"min\" is similar to existing symbol \"Min\". More…$

Out[22]=

That defined min to be the minimum value, and to be the rule table giving the values of and :

In[23]:=

Out[23]=

This was the function we were trying to fit:

In[24]:=

Out[24]=

And we can connect the general function to the specific values of and by using the /.
operator. (You can also use the ReplaceAll function. The /. is short-hand for ReplaceAll.)

In[25]:=

Out[25]=

In[26]:=

Out[26]=

If you want to define a function representing the fit:

In[27]:=

Out[27]=

In[28]:=

Out[28]=

The Minimize function works algebraically, which means it sometimes doesn't do quite what you'd like. It generally works well on polynomial problems, but if you give it a nasty enough trancendental problem, you're out of luck.

In[29]:=

Out[29]=

So, sometimes you get better results working just numerically. For that, try NMinimize .

In[30]:=

Out[30]=

Here's our linear least squares fit again:

In[31]:=

Out[31]=

Another numerical function is FindMinimum, which uses a different numerical algorithm. You have to specify a starting point for each unknown variable.

In[32]:=

Out[32]=

The Fit function does exactly this same minimization conceptually, but it only works if the fit function looks like

and the are the only unknowns. This is the traditional method of curve fitting (predating modern computers that can do more powerful techniques almost as fast) because if has this form, you can take a short cut from linear algebra and do the computation very quickly. Otherwise, the minimization can be computationally intensive and may get stuck at a local minimum instead of finding the global minimum.

Non-linear least squares

The linearization method

To do non-linear curve fitting with least squares, there are a couple of alternatives. One is to linearize the data first, then proceed using Fit.

As before, let's make up some noisy data to play with. It's basically $FormBox[RowBox[{4, RowBox[{x, ^, 2.2}]}], TraditionalForm]$ with noise added to the coefficient and the exponent.

In[33]:=

RowBox[{nonlinearData, =, RowBox[{Table, [, RowBox[{RowBox[{{, RowBox[{x, ,, RowBox[{(4 + Rand ... }], ]}]}], )}]}]}]}], }}], ,, , RowBox[{{, RowBox[{x, ,, 1, ,, 10, ,, 0.25}], }}]}], ]}]}]

Out[33]=

RowBox[{{, RowBox[{RowBox[{{, RowBox[{1, ,, 4.92824}], }}], ,, RowBox[{{, RowBox[{1.25, ,, 6.3 ... ,, RowBox[{{, RowBox[{9.75, ,, 460.075}], }}], ,, RowBox[{{, RowBox[{10., ,, 518.81}], }}]}], }}]

In[34]:=

[Graphics:HTMLFiles/CurveFittingHowTo_94.gif]

Out[34]=

We'd like to fit this to a power function and find and .

In[35]:=

Out[35]=

But we can't use Fit, because the unknowns aren't in the right place. So, we linearize the data first. Assuming the power function is correct for our data, we can take the logarithm, and get something in the right form for Fit:

So even though our data is not in the right form for Fit, it turns out that is in the right form. Here's an incantation to linearize the data. The trick is that /. can apply rules that involve patterns (see the Mathematica book 2.5 ), so this next command looks at and replaces anything that looks like with . As in function definitions, the _ on the x and y indicates that these are pattern variables. Without the _, Mathematica will think you mean to replace only stuff with the symbols x and y. And you don't use the _ on the right hand side of the rule or in a function definition, only on the left.

In[36]:=

$linearizedData = nonlinearData/.{x_, y_}  {Log[x], Log[y]}$

Out[36]=

RowBox[{{, RowBox[{RowBox[{{, RowBox[{0, ,, 1.59498}], }}], ,, RowBox[{{, RowBox[{0.223144, ,, ... ox[{{, RowBox[{2.27727, ,, 6.13139}], }}], ,, RowBox[{{, RowBox[{2.30259, ,, 6.25154}], }}]}], }}]

In[37]:=

[Graphics:HTMLFiles/CurveFittingHowTo_109.gif]

Out[37]=

Now we can use Fit:

In[38]:=

Out[38]=

In[39]:=

[Graphics:HTMLFiles/CurveFittingHowTo_114.gif]

Out[39]=

In[40]:=

[Graphics:HTMLFiles/CurveFittingHowTo_117.gif]

Out[40]=

And you can see that this is pretty close to $FormBox[RowBox[{4, RowBox[{RowBox[{x, ^, 2.2}], :}]}], TraditionalForm]$

In[41]:=

Out[41]=

$RowBox[{4.2303, , RowBox[{x, ^, 2.16518}]}]$

In[42]:=

[Graphics:HTMLFiles/CurveFittingHowTo_123.gif]

Out[42]=

In[43]:=

[Graphics:HTMLFiles/CurveFittingHowTo_126.gif]

Out[43]=

The direct least squares method

Since Mathematica can directly minimize various expressions, we can also skip the linearization step and minimize the error directly:

In[44]:=

Out[44]=

In[45]:=

Out[45]=

$RowBox[{6.67436, , RowBox[{x, ^, 1.94624}]}]$

In[46]:=

[Graphics:HTMLFiles/CurveFittingHowTo_133.gif]

Out[46]=

In[47]:=

[Graphics:HTMLFiles/CurveFittingHowTo_136.gif]

Out[47]=

And you should be able to see that the function found by the linearization method isn't quite the same as the one found by the direct method:

In[48]:=

Out[48]=

$RowBox[{{, RowBox[{RowBox[{4.2303, , RowBox[{x, ^, 2.16518}]}], ,, RowBox[{6.67436, , RowBox[{x, ^, 1.94624}]}]}], }}]$

Both functions are actually the optimum fit to the data, but under different notions of distance. And notice that neither one is exact compared to what we started with. For example, here's what I got on one run of this worksheet:

Out[55]=

$RowBox[{{, RowBox[{RowBox[{3.5498, , RowBox[{x, ^, 2.27148}]}], ,, RowBox[{3.0792, , RowBox[{x, ^, 2.34363}]}]}], }}]$

Since the data set is constructed with random noise, the results will be a little different each time you run it. But neither of these gives back $FormBox[RowBox[{4, , RowBox[{x, ^, 2.2}]}], TraditionalForm]$ exactly. (Think about it: Should they?) And which curve is "better"?

This contention between the results illustrates the fundamental conceptual problems in curve fitting: (1) Guess the appropriate form of the function. (2) Determine an appropriate notion of "distance" between the curve and the data to minimize.

Maximum likelihood

An alternative notion of distance that is appropriate for modeling changing probabilities is likelihood. This notion assumes that the data is of the form where is an independent variable, such as distance or time, are independent random numbers, and are the parameters that we want to find. Then, the likelihood of the data is the probability of getting exactly the 's. The curve fit procedure is to determine values of the parameters such that the likelihood of the data is maximal.

As an example, let's suppose we have a biological experiment that succeeds or fails, for example, getting bacteria to accept a fragment of DNA. Let's suppose that the probability of success depends on temperature . Furthermore, let's suppose that we have some knowledge of the biochemistry involved that tells us that the probability of success is actually an exponential function: where and are unknown. We are given results from experiments run at different temperatures, and they are simply given as success or failure, and our job is to find and .

First, let's invent some data, using and .

In[49]:=

Out[49]=

Random returns a random number between 0 and 1, so the test Random[] < p returns True with probability and False with probability , so we can use it to simulate our experiment. We'll also assume that this experiment is fairly expensive and time consuming, so we can't run zillions of experiments.

In[50]:=

In[51]:=

Out[51]=

{{0, True}, {2, True}, {4, True}, {6, True}, {8, True}, {10, True}, {12, False}, {14, False}, ... False}, {68, False}, {70, True}, {72, False}, {74, False}, {76, False}, {78, False}, {80, False}}

Here's a way to plot that data. Do you see how this command works?

In[52]:=

[Graphics:HTMLFiles/CurveFittingHowTo_163.gif]

Out[52]=

The data we have isn't points which is what we'd need to do traditional curve fitting. In other words, we want to fit a curve but we don't have points from the curve plus noise like we did in earlier examples; we have something else entirely. Intuitively, it seems impossible for least squares to give anything useful for this type of data, so instead, we do maximum likelihood. The experiments are independent, so the probability of getting all this data is the product of the probabilities of getting each point. But the probability of getting each point depends on and .

In[53]:=

$likelihood[data_, a_, b_] := Product[If[data[[j, 2]], pSuccess[data[[j, 1]], a, b], 1 - pSuccess[data[[j, 1]], a, b]],  {j, 1, Length[data]}]$

So for example:

In[54]:=

Out[54]=

In[55]:=

Out[55]=

These are tiny numbers, and that causes trouble with the numerical maximization process, so instead of maximizing the likelihood, we maximize the log likelihood (Think about it: Why can we do this?)

We could do this, but then Mathematica will compute that tiny likelihood, then take the log.

In[56]:=

A better way to compute the same thing is to expand the log of the product into a sum of logs. I'll do this computation using different notation:

In[57]:=

$logLikelihood[data_, a_, b_] := Total[data/.{x_, success_} If[success, Log[pSuccess[x, a, b]], Log[1 - pSuccess[x, a, b]]]]$

Just to check that we did this right, these should be the same number:

In[58]:=

Out[58]=

In[59]:=

Out[59]=

Here's the first try at running the fit:

In[60]:=

Out[60]=

$Maximize[{Log[^(-a (2 - b))] + Log[^(-a (4 - b))] + Log[^(-a (6 - b))] ... a (76 - b))] + Log[1 - ^(-a (78 - b))] + Log[1 - ^(-a (80 - b))], a>0}, {a, b}]$

Which means it couldn't solve the problem algebraically. So, let's try the numerical methods:

In[61]:=

Out[61]=

$NMaximize[Log[^(-a (2 - b))] + Log[^(-a (4 - b))] + Log[^(-a (6 - b))] ... 63309;^(-a (76 - b))] + Log[1 - ^(-a (78 - b))] + Log[1 - ^(-a (80 - b))], {a, b}]$

You probably got an error message, either that an overflow occurred, or that it got a complex number somewhere along the way. That means that NMaximize is trying values of and that yield logs of negative numbers, or perhaps log of 0. Let's use the constraint feature of NMaximize to give it some additional hints: We ask it to maximize the log likelihood, but subject to some reasonable constraints. We know the exponential should decrease as increases, so we add in .

In[62]:=

Out[62]=

Sometimes that works, sometimes it doesn't, depending on what random numbers appeared in our simulated experiment. Let's try FindMaximum since it takes a starting point.

In[63]:=

Out[63]=

That probably didn't work because we get something like somewhere if we start at

In[64]:=

FindMaximum :: lstol : The line search decreased the step size to within tolerance specified b ... need more than MachinePrecision digits of working precision to meet these tolerances. More…

Out[64]=

This is pretty good, at least the time I ran it. Sometimes you have to poke around with different starting points to get reasonable results. There are also zillions of options, and you can spend lots of time playing with them, tweaking the numerical method, but unless you're desperate or know what all the tweaks mean, doing that is often a waste of time.

The result isn't perfect, but it has a definite interpretation: These values for and are the ones such that the probability of getting our observations is maximal. And they're reasonably close to the exact answer, which is great given how little information our data acutally contains.

Created by Mathematica (January 20, 2005)